微言 | wyanassert
个人工作总结

博客内容主要是 iOS 技术分享, 以及随笔.

PNG 文件结构解析

发表于 分类于
本文字数： 7.3k 阅读时长 ≈ 7 分钟

PNG 的二进制文件由文件头(文件署名域, 决定文件类型)加上多个块组成, 其中每个块又有四个部分, 如下:

名称 字节数 说明
Length（长度） 4字节 指定数据块中数据域的长度, 其长度不超过（231- 1）字节
Chunk Type Code（数据块类型码） 4字节 数据块类型码由ASCII字母（A-Z和a-z）组成
Chunk Data（数据块数据） 可变长度 存储接照Chunk Type Code指定的数据
CRC（循环冗余检测） 4字节 存储用来检测是否有错误的循环冗余码

实际具体

我们有一张名为 test.png 的图片, 尺寸是 6*8, 先使用 xxd 命令输出二进制信息

1
xxd test.png > test.hex

使用 VSCode 等编辑器打开, 大致如下

1
2
3
4
5
6
00000000: 8950 4e47 0d0a 1a0a 0000 000d 4948 4452  .PNG........IHDR
00000010: 0000 0006 0000 000a 0103 0000 00ad c0bd  ................
00000020: 7000 0000 0350 4c54 4500 0000 a77a 3dda  p....PLTE....z=.
00000030: 0000 0014 4944 4154 785e 6dc0 8100 0000  ....IDATx^m.....
00000040: 0080 a0fd a917 a860 0014 0001 9406 ce62  .......`.......b
00000050: 0000 0000 4945 4e44 ae42 6082            ....IEND.B`.
  • 文件头 8950 4e47 0d0a 1a0a
    • 前面个字节是文字头, 标志文件是个 PNG
  • IHDR, 包含了关于图像基本属性的信息
    • 0000 000d 前四个字节描述了 IHDR 的大小是 13 字节
    • 4948 4452 是 IHDR 名字
    • 后面 13 个字节是 IHDR 数据
      • 0000 0006 四字节, 是图片宽为 6
      • 0000 000a 四字节, 图片高为 10
      • 01 1 字节, 指定每个样本的位深度, 即每个像素的颜色深度
      • 03 1 字节, 指定图像的颜色类型, 如灰度图、真彩色图等
      • 00 1 字节,指定图像的压缩方式, PNG目前只定义了一种压缩方式
      • 00 1 字节, 指定图像的滤波方式
      • 001 字节, 指定图像的交错方式, 用于渐进式显示
    • ad c0bd 70 表示对 IHDR 的校验和
  • PLTE, 调色板
    • 00 0000 03 表示 PLTE 数据只有 3 字节
    • 50 4c54 45 表示调色板的名字 PLTE
    • 00 0000 PLTE 的数据
    • a77a 3dda PLTE 校验和
  • IDAT
    • 0000 0014 表示图像数据只有 20 字节
    • 4944 4154 IDAT 名字
    • 785e 6dc0 8100 0000 0080 a0fd a917 a860 0014 0001 图像数据
    • 9406 ce62 IDAT 校验和
  • IEND
    • 0000 0000 表示 IEND 数据 0 字节
    • 4945 4e44 IEND 名字
    • ae42 6082 IEND 校验和

可见本来这张图 6*8 的尺寸需要 6*8*4 192 字节, 但是经过Deflate算法压缩到了 20 字节, (不过本来这张图就是一张纯黑图, 压缩率高是正常的), 然后额外信息是 72 字节.

Deflate

参考文章:Gzip 格式和 DEFLATE 压缩算法

DEFLATE 是最广泛的无损压缩算法, 结合了 LZ77 算法和 Huffman 编码, 由 Phil Katz 设计, 并被 RFC1951 标准化.

LZ77 算法

基本原理

我们平时使用的文件总是会有很多重复的部分, LZ77 压缩算法正是利用了这一点. 它会试图尽可能地找出文件中重复的内容, 然后用一个标记代替重复的部分, 这个标记能够明确地指示这部分在哪里出现过. 举个例子,

Four score and seven years ago our fathers brought forth, on this continent, a new nation, conceived in Liberty, and dedicated to the proposition that all men are created equal.

我们可以找出不少重复的片段. 我们规定, 只要有两个以上的字符与前文重复, 就使用重复标记 <d,l> 代替它. <d,l> 表示这个位置的字符串等价与 d 个字符前, 长度为 l 的字符串. 于是上面的内容就可以表示为:

Four score and seven years ago <30,4>fathe<16,3>brought forth, on this continent, a new nation,<25,4>ceived in Liberty<36,3><102,3>dedicat<26,3>to<69,3>e proposi<56,4><85,3>at all m<138,3>a<152,3>cre<44,5>equal.

实现这个算法最简单的方式就是遍历字符串, 对于每个字符都在前文中顺序查找是否有重复的字符, 然后求出最长重复子串. 这种做法时间复杂度为 O(n^2), 效率较低, 特别是在处理大文件的时候. 为了提高效率, 我们使用哈希表和滑动窗口优化.

使用哈希表

举个例子, 考虑字符串 abcabcdabcde, 算法运行时有以下几步:

  1. 扫描到第 0 个字符 a, 哈希表为空, 原样输出字符 a, 并且将字符串 abc 插入哈希表中. 
    1
    2
    3
    4
    hash table: {}
    abcabcdabcde
    ^
    output: a
  2. 扫描到第 3 个字符 a, 哈希表指示 abc 在 0 处出现过. 最长的匹配就是 abc, 因此输出 <3,3>. 同时把当前位置插入到 abc 映射的列表中. 
    1
    2
    3
    4
    hash table: {"abc":[0],"bca":[1],"cab":[2]}
    abcabcdabcde
       ^
    output: abc<3,3>
  3. 扫描到第 7 个字符 a, 哈希表指示 abc 在 0, 3 处出现过. 依次与当前位置匹配, 0 处只能匹配到 abc, 而 3 处能匹配到 abcd, 最长的匹配为 abcd, 于是输出 <4,4>. 同时把当前位置插入到 abc 映射的列表中. 
    1
    2
    3
    4
    hash table: {"abc":[0,3],"bca":[1],"cab":[2],"bcd":[4],"cda":[5],"dab":[6]}
    abcabcdabcde
           ^
    output: abc<3,3>d<4,4>
    zlib 中这个哈希表的实现非常精妙, 关于它的详细实现超出了本文的讨论范围.

滑动窗口

即使有了哈希表, 过长的文件仍然会导致效率问题. 为此我们使用滑动窗口, 查找重复内容时仅在窗口中查找. 窗口的长度是固定的, 通常是 32KB. 在 zlib 的实现中, 使用一个两倍窗口大小的缓冲区, 如下所示:

1
2
|-------search-------+------lookahead-----|
  1. 初始时将待压缩数据填入缓冲区, 指针位于缓冲区的开始处;
  2. 随后指针向后扫描, 对数据进行压缩.
  3. 我们把指针扫描过的的部分称为 search 区, 未扫描过的部分称为 lookahead 区.
  4. 于每个扫描的字符, 算法都只会在 search 区中寻找匹配.
  5. 当 lookahead 区长度不足(小于一个固定值)时, 算法就会移动窗口以继续扫描更多的数据.
  6. 具体的做法时将缓冲区后半部分的数据复制到前半部分并移动指针, 然后在缓冲区的后半部分读入新数据, 接着还要更新哈希表, 因为数据的位置发生了改变.

惰性匹配(lazy matching)

有的时候这种策略并不能得到最优的压缩结果. 举个例子, 考虑字符串 abcbcdabcda, 当扫描到第 6 个字符的时候, 哈希表指示 abc 在 0 处出现过, 最长匹配为 abc, 于是输出 <6,3>; 后面的 da 没有与之重复的内容, 原样输出. 因此压缩的结果是 abcbcd<6,3>da. 然而在第 7 个字符的位置能在前文找到一个更长的匹配 bcda, 更好的压缩结果应该是 abcbcda<4,4>.

为了解决这个问题, DEFLATE 采用一叫做惰性匹配的策略优化. 每当算法找到一个长度为 N 的匹配后, 就会试图在下一个字符寻找更长的匹配. 只有当没有找到更长的匹配时, 才为当前匹配输出重复标记; 否则就会丢弃当前匹配, 使用更长的匹配. 注意惰性匹配可以连续触发, 如果一次惰性匹配发现了更长的匹配, 仍会继续进行惰性匹配, 直到无法在下一个字符找到更长匹配为止. 惰性匹配能够提高压缩率, 但是会让压缩变慢.

Huffman 编码

如果我们真的使用 <d,l> 这样的格式表示重复的内容, 那就太愚蠢了. 首先是这样的格式太占空间了, 其次这种格式让尖括号变成了特殊字符, 还得设法转义它们. 那么应该如何表示重复部分距离和长度呢? DEFLATE 的做法是使用 Huffman 编码对数据重新编码.

Huffman 编码由美国计算机科学家 David A. Huffman 于 1952 年提出, 它是根据字符出现频率构造而成的前缀编码. 与我们平时常用的固定位编码(每个字符占 8 位)不同, Huffman 编码中每个字符的编码的位数都可能不同, 却能够明确地区分每个字符, 不会有任何歧义.

前缀编码

为什么每个字符占的位数都不同却能明确地区分它们呢? 这就是前缀编码的作用. 为了说明什么是前缀编码, 试想我们在打电话. 电话号码的长度是不一样的: 有三位的, 如 110, 119; 有五位的, 如 10086, 10010; 有 7 位或 8 位的固定电话, 又有 11 位的手机号码等等. 然而拨号的时候依次输入号码, 总能正确识别 (固定电话摘机拨号无需按呼叫键). 这是因为除了匪警 110 之外不会有任何一个电话号码以 110 开头, 任何一个固定电话号都不可能是某个手机号的前缀. 电话号码就是一种前缀编码. 所以, 虽然 Huffman 编码中每个字符的编码位数都不同, 但是短的编码不会是长的编码的前缀. 这样就保证了 Huffman 编码没有歧义.

我们使用 Huffman 树构造 Huffman 编码. 前文说了, Huffman 编码有长有短, 那么显然让使用频率高的字符编码短, 使用频率低的字符编码长比较合理. 假设我们要对字符 a, b, c, d, e 进行编码, 它们的使用频率如下表所示:

character times
a 1
b 4
c 4
d 3
e 1

构造方式非常简单. 我们把字符的出现频率视为优先级, 放入一个最小优先队列中:

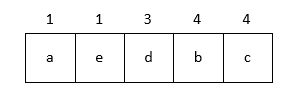
然后弹出两个优先级最低的字符作为子节点, 构造出第一个二叉树; 父节点的优先级视为两个字节优先级之和, 然后把父节点插入队列中: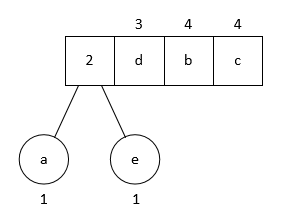

重复这个操作, 最后我们会得到一颗二叉树. 这便是 Huffman 树.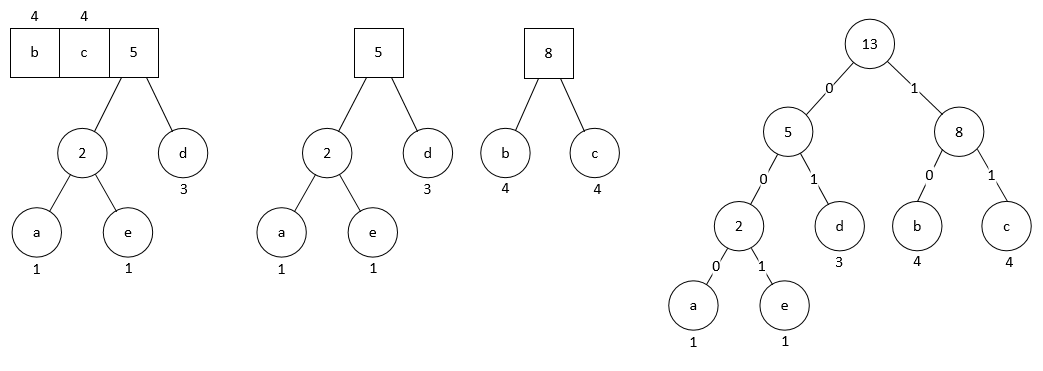

我们把这棵树的左支编码为 0, 右支编码为 1, 那么从根节点向下遍历到叶子节点, 即可得出相应字符的 Huffman 编码. 因此我们得到上面例子的 Huffman 编码表为:

character code
a 000
b 10
c 11
d 01
e 001

假设有字符串 badbec, 使用 Huffman 编码后得到 10000011000111. 解码也很简单, 依次读入每个比特, 利用 Huffman 树, 自根节点开始逢 0 向左逢 1 向右, 到达叶子节点即输出相应的字符, 然后回到根节点继续扫描.

对距离和长度进行编码

一个字节有 8 位, 因此我们需要 0 至 255 一共 256 个 Huffman 编码. 统计文件各个字符的使用频率, 构造出 Huffman 树即可计算出这 256 个编码. 那么如何用 Huffman 编码表示重复标记中的距离和长度呢? DEFLATE 算法是这样做的:

  • 对于距离, 它有 0 至 29 一共 30 个编码. 距离编码的含义如下表所示:

    code extra distance code extra distance code extra distance
    0 0 1 10 4 33-48 20 9 1025-1536
    1 0 2 11 4 49-64 21 9 1537-2048
    2 0 3 12 5 65-96 22 10 2049-3072
    3 0 4 13 5 97-128 23 10 3073-4096
    4 1 5,6 14 6 129-192 24 11 4097-6144
    5 1 7,8 15 6 193-256 25 11 6145-8192
    6 2 9-12 16 7 257-384 26 12 8193-12288
    7 2 13-16 17 7 385-512 27 12 12289-16384
    8 3 17-24 18 8 513-768 28 13 16385-24576
    9 3 25-32 19 8 769-1024 29 13 24577-32768

    每个编码都表示一个或多个距离. 当它表示多个距离时, 意味着接下来会有 extra 位表示具体的距离是多少. 例如假设编码 14 接下来的 6 位为 011010, 则表示距离为 129 + 0b011010 = 129 + 26 = 155. 这样距离编码能表示的距离范围为 1 至 32768.

  • 对于长度, 它与普通字符共用同一编码空间. 这个编码空间一共有 286 个编码, 范围是从 0 至 285. 其中 0 至 255 为普通字符编码, 256 表示压缩块的结束; 而 257 至 285 则表示长度. 长度编码的含义如下表所示:

    code extra length(s) code extra length(s) code extra length(s)
    257 0 3 267 1 15,16 277 4 67-82
    258 0 4 268 1 17,18 278 4 83-98
    259 0 5 269 2 19-22 279 4 99-114
    260 0 6 270 2 23-26 280 4 115-130
    261 0 7 271 2 27-30 281 5 131-162
    262 0 8 272 2 31-34 282 5 163-194
    263 0 9 273 3 35-42 283 5 195-226
    264 0 10 274 3 43-50 284 5 227-257
    265 1 11,12 275 3 51-58 285 0 258
    266 1 13,14 276 3 59-66

    与距离编码类似, 每个编码都表示一个或多个长度, 表示多个长度时后面会有 extra 位指示具体的长度. 长度编码能表示的长度范围为 3 至 258.

解压时, 当读到编码小于等于 255, 则认为这是个普通字符, 原样输出即可; 若在 257 至 285 之间, 则说明遇到了一个重复标记, 这意味着当前编码表示的是长度, 且下一个编码表示的是距离. 解码得到长度和距离, 再在解压缓冲区中找到相应的部分输出即可; 若为 256, 则说明压缩块结束了.

Huffman 编码表的存储

我们知道, Huffman 编码是根据字符的出现频率构造的. 不同的文件字符出现的频率都不同, 因此 Huffman 编码也不同. 为了能够正确地解压, 压缩块中还必须存储 Huffman 编码表. 这一节我们来讨论如何用最小的空间存储这个 Huffman 编码表.

将 Huffman 编码表表示为长度序列

为了高效地存储 Huffman 编码表, DEFLATE 算法规定, Huffman 树的每一层的叶子节点必须从这一层的最左侧开始, 按照 Huffman 编码的数值大小从小到大依次排列; 内部节点排列在随后. 此外同一层的字符应该按照字符表(如 ASCII 码表)的顺序依次排列. 这样 3.1 节中的 Huffman 树就应该调整为: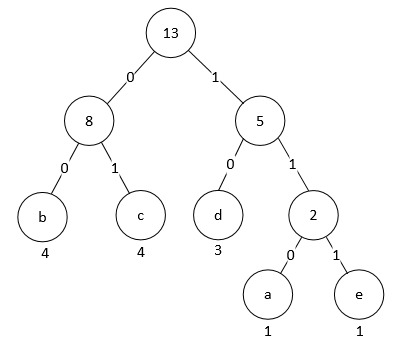

调整后的 Huffman 编码表就是:

character code
a 110
b 00
c 01
d 10
e 111

注意调整后的 Huffman 编码并不影响压缩率: 各个字符编码的长度不变, 最常用的字符的编码仍是最短的. 不难发现, 相同长度的编码都是依次递增的, 且某个长度的编码的最小值取决于上个长度的编码的最小值和数量. 现设长度为
i 的编码的最小值为 mi, 有 ni 个; 又设长度为 0 的编码的最小值为 0, 有 0 个. 那么易得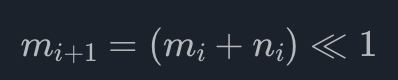

这里的 “<<” 表示左移. 这样, 我们只需要知道每个字符的 Huffman 编码长度, 即可推算出所有字符的 Huffman 编码了. 对如上面的例子, 我们只需存储长度序列 <3,2,2,2,3> 即可. 解压时扫描这个序列, 得到各个长度的编码的数量, 即可求算出各个长度的编码的最小值; 相同长度的编码都是依次递增的, 所以依次加一, 即可得出所有字符的 Huffman 编码. 特别地, 长度 0 表示这个字符没有在压缩块中出现过, 构造 Huffman 编码的时候会排除它.

对长度序列编码

长度序列中很容易出现连续重复的值; 并且由于文件中可能有很多未使用的字符, 也会出现很多 0. 因此 DEFLATE 会对这个长度序列编码, 如下所示:

code meaning
0-15 表示长度 0 至 15
16 前面的长度重复 3 到 6 次. 接下来的两位指示具体重复多少次, 这与 3.2 节中的长度和距离编码类似.
17 长度 0 重复 3 至 10 次. 接下来的 3 位指示具体重复多少次.
18 长度 0 重复 11 至 138 次. 接下来的 7 位指示具体重复多少次.

使用 Huffman 编码压缩 Huffman 编码表

将 Huffman 编码表表示成编码后的长度序列已经比较精简了, 但是 DEFLATE 算法认为这还不够. 它决定对这个编码后的长度序列再次使用 Huffman 编码压缩. 这一步就有一点点绕了. 为了做到这一点, 我们需要为长度序列的编码 – – 0 至 18, 构造 Huffman 编码表(然而这个长度序列表示的就是一个 Huffman 编码表, 等于我们是在为一个 Huffman 编码表构造 Huffman 编码表). 问题来了, 怎么表示这个 Huffman 编码表的 Huffman 编码表呢? 首先, DEFLATE 算法定义了一个神秘数组:

因为有可能不是所有的长度都能用上, 因此我们会先用一个数字标识使用这个数组中的前 k 个编码. 例如长度序列编码只使用了 2, 3, 4, 16, 17, 则 k = 16. 接下来会有 k 个数字, 第 i 个数字表示长度序列编码 A[i] 的 Huffman 编码的长度, 0 表示相应的编码未使用. 因为只要知道了每个字符的 Huffman 编码长度, 就能推算出所有字符的 Huffman 编码. 这样我们就得到了编码后的长度序列的 Huffman 编码表.

在压缩数据中先存储编码后的长度序列的 Huffman 编码表, 紧接着再存储编码后的长度序列的 Huffman 编码数据. 这样我们就在压缩块中用较小的空间存储了压缩数据的 Huffman 编码表.

-------------本文结束感谢您的阅读-------------
相关文章

欢迎关注我的其它发布渠道